[리뷰] 소름 돋는 수학의 재미 (상편)
in Review on Review, Book, 수학, 재미, 기발, 흥미로운, 문제, 방정식, 수열, 무한, 유리수, 무리수, 비밀, 가설

미디어숲출판사의"소름 돋는 수학의 재미 (상편)(천융밍 저/김지혜 역)"를 읽고 작성한 리뷰입니다.

기발하고 흥미롭고 때로는 미스터리한 수학 문제들을 소개하는 책으로 수학의 오묘함과 무한한 재미를 느낄 수 있게 해주는 양서이다.
수학을 싫어하는 사람도 재미를 느낄만한 문제들이 어림잡아도 50개는 넘게 소개되고 있다. 각 단원은 크게 4개로 나뉘어져 유리수, 무리수, 방정식, 수열과 극한으로 나뉜다.
완전하게 기억나진 않겠지만 그래도 우리가 대부분 중학교까지 배웠던 수학의 기초 정도만 이해하고 있으면 읽기 무리 없는 수준으로 구성되어 있지만 그 깊이는 아직까지도 풀리지 않는 미스테리까지 이어지기에 아는 지식으로 진리의 극한을 느끼는 재미가 있다.
만약 우리가 복소수의 세계를 접하거나 물리학이나 양자 역학 같이 이미 수식이나 기호부터 알 수 없는 세계에서 수학을 느끼고자 한다면 갑갑함을 느끼고 이내 책을 덮을 수 밖에 없게 된다.
이상한 기호와 수식에서 이미 의사소통이 이뤄지지 않기 떄문이다. 깊이 있는 진리에 도달하는 방법이 순수한 사고와 노력에 의한 것이 아니라 애초에 의사소통이 안되어 외국어로 수학을 접하는 느낌이 든다면 절망적일 것이다.
그렇지만 이 책은 우리가 누구나 알고 있는 사칙 연산과 수식을 기본으로 사고를 확장해 나가는 구성이기에 상당히 쉽게 시작하여 어렵게 끝이 나는 해볼만한 모험을 담고 있다는 것이 눈에 띄는 장점이라 하겠다.
특히 1장 유리수 파트는 정말 도전해봄직하다. 이어지는 무리수는 무한의 속성이 포함되어 있기에 만만치 않은 세계가 하나 더 튀어 나오는 셈이고, 방정식의 경우도 대수적 지식이 추가된다. 마지막 수열과 극한도 새로운 공식이 등장하거나 무한의 세계를 대수적으로 해석해야 하는 단계가 등장한다.
그렇기에 비교적 많은 제약과 지식이 필요없는 유리수의 세계를 접하다보면 이 책이 말하고자 하는 바를 이해할 수 있을 것이다. 그리고 그 재미를 이해하게 된다면 하나씩 더 깊이 있는 수학 문제의 모험을 떠날 준비가 될 것이라 생각한다.
이 책에서 소개되는 50가지의 문제들은 불과 몇페이지 정도에 지나지 않는다. 짧게는 3페이지에서 길어도 10페이지 안쪽으로 마무리 되기에 가장 흥미롭고 평소 궁금했던 문제부터 읽어나가면 될 것이다.
모든 것을 리뷰에서 다 소개할 순 없기에 유리수를 중심으로 흥미로웠던 문제를 소개해 보겠다.
신비한 두 그룹의 숫자들이 있다.
123789, 561945, 642864 242868, 323787, 761943
이 그룹의 합은 서로 같다.
123789 + 561945 + 642864 = 242868 + 323787 + 761943 = 1328598
더 재미있는 것은 제곱의 합도 같다.
123789^2 + 561945^2 + 642864^2 = 242868^2 + 323787^2 + 761943^2
더 놀라운 것은 첫번째 수를 지운 후에도 그룹의 합이 같다.
23789 + 61945 + 42864 = 42868 + 23787 + 61943 = 128598
그것들의 제곱합도 같다. 다시 첫번째 수를 지운 후 4자리의 숫자끼리의 합도 같고 역시 제곱합도 같다. 그렇게 계속 한자리가 남을 때까지 숫자를 줄인후에도 역시 합은 물론 제곱합까지 같다.
9 + 5 + 4 = 8+ 7+ 3 = 18
마지막으로 6자리의 수에서 마지막 한 자리씩 지워나가며 합과 제곱합을 취한 결과도 계속 동일하다. 신기하지 않은가? 왜 이런 현상이 일어나는지 파악하다보면 수학의 한 분야인 정수론에 다다른다고 한다.
수학을 이렇게 흥미로운 길로 접근한다면 정수론이든 해석학이든 집합론이든 진입하는데 큰 어려움을 느끼지 않을 것이다. 아마도 유별난 천재가 아닌 이상 대부분의 수학자들도 이런 호기심의 문을 열며 수학의 세계로 들어간 것이 아닐까 생각한다.
그 외에도 책에는 온갖 신기한 문제들로 가득하다. 동일하지 않은 세자리 수를 3단계의 가공을 거치면 늘 495의 결과가 나오는 카프리카 블랙홀의 문제부터 루트 2를 직접 계산하는 방법을 살피며 재귀식으로 나타나는 연분수도 등장한다. 
단순히 재미를 추구하는 문제만 나오는 것은 아니다. 소수 가설 파트에서는 귀류법이라는 진리를 밝히는 무에서 유를 창조하는 논리 혹은 증명법이 소개되는가 하면 우리의 숫자 세기가 만을 넘어가면 만진법을 따르기에 읽기가 불편하다는 새로운 깨달음을 얻을 수도 있다.
논리적으로 궤변임에도 쉽게 반박하기 어려운 제논의 역설을 파훼하는 증명법을 알아보기도 하며 0.9999… = 1이라는 공식을 파헤치며 라마누잔 합이라는 개념을 살피기에 철학과 논리에 까지 닿아있다 할 수 있다. 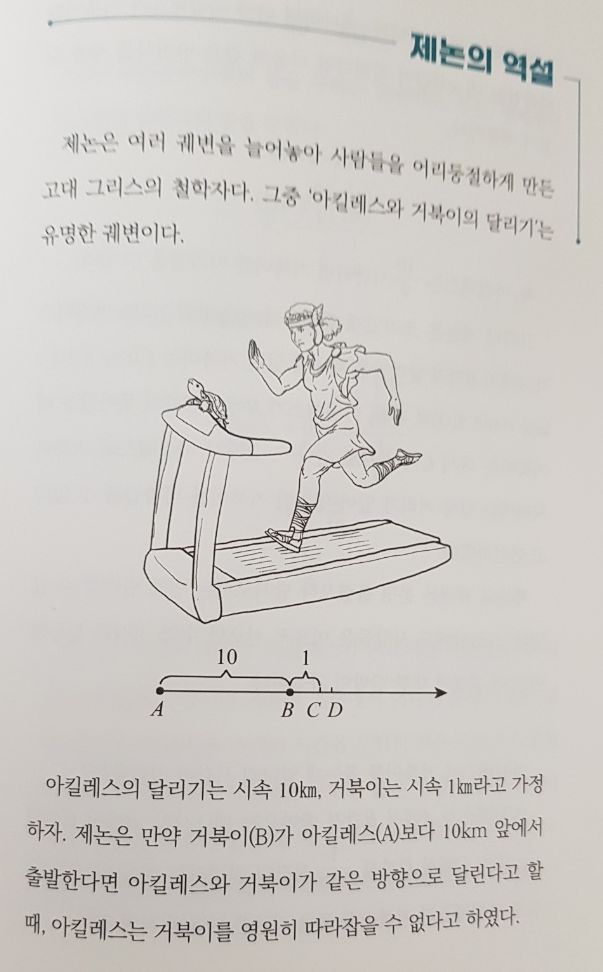
이 책은 특히 자라나는 청소년들이 스스로의 생각의 깊이를 넓히고 진리 추구의 재미를 느끼게 하는데 큰 도움이 될 책이라는 생각이 든다. 일반 성인들도 잠시 신비로운 세계로 모험을 떠나는 기분을 느낄 수 있기에 반드시 추천하고 싶은 도서이다.
YES24 리뷰어클럽 서평단 자격으로 작성한 리뷰입니다.
