더퀘스트 출판사의 "미적분의 쓸모(한화택 저)"를 읽고 작성한 리뷰입니다.

---

미적분이 무엇인지를 설명하기에 앞서 어디에 쓰이는지를 살펴보는 책으로 미적분에 대한 흥미를 가질 수 있음은 물론 일상에서 구체화된 모습을 보며 이해를 높일 수 있다는 점이 장점이다.

추상화된 논리를 그림으로 그리며 구체화할 수 있다면 즉, 우리 눈으로 볼 수 있게 된다면 막연했던 보이지 않던 실체는 제법 만만한 지식으로 다가온다.

그 막막했던 개념들이 손에 잡힐 듯 다가온 상태에서 우리가 일상에서 궁금했던 것들을 이 개념들을 통해 풀 수 있다는 실마리가 어렴풋이 보이면 진리에 대한 지적 욕구가 솟구치는 것은 물론 커다란 흥미를 느낄 수 있다.

이 책은 이처럼 하늘 높은 곳에 숭고했던 진리를 우리 주변의 일상으로, 땅으로 끌고 내려와 친숙하게 만들어 주는 책으로 그 중 미적분에 대한 주제를 다루고 있다.

미적분이 공학이나 일상에서 자주 활용되는 분야인 최적화, 기울기, 기하학, 역학, 예측 등 다양한 케이스를 다루고 있지만 모든 것을 담기엔 분량이 부족하여 일반인들이 최근 알파고로 친숙해진 최적화를 중심으로 리뷰를 정리해본다.

중고교 시절 한때나마 수학을 좋아했던 학생으로써 주변 어른들로부터 늘 듣던 말이 있다.

“수학, 그 까짓거 거스름돈 계산할 때나 쓰지.. 배워서 뭐한다고.. “

사회에 나와 직장을 다니며 이 말이 사실임을 깨닫는 10년 동안 허탈하기 그지 없었다. 대학이나 취업을 위한 평가를 위한, 교육을 위한 교육에 전념한 자신을 탓하기도 하며 이런 교육과정을 설계한 교육부를 원망하기도 했고 쓸데도 없는 지식을 익히게 하는 기업에 불평을 쏟아내기도 했다.

그리고 이번에는 직장에 적응하며 경력을 쌓아올리며 어른들이 했던 그 말이 거짓임을 깨닫는데 10년을 보냈다.

기껏 10년 동안 수학이 거스름돈 계산할 때나 쓰는 살면서 불필요한 지식임을 깨달아 놓고 그 후 10년 동안 그 말이 거짓이라는 사실을 깨달았으니 20년이 지났는데 수학을 바라보는 자세는 원점이 된 느낌이다. 진리의 세계는 참 오묘하다는 생각이 들었다.

계기는 바로 알파고가 등장하면서 부터다. AI라는 것이 무엇이기에 바둑이라는 무한에 가까운 경우의 수를 무너뜨린단 말인가? 이세돌의 무기이자 자랑인 상대를 흔드는 승부호흡, 감으로 재단되는 대국판 위의 판세 그 무엇도 AI의 철두철미한 계산력 앞에는 미래를 내다볼 수 있는 경우의 수 앞에서는 무용지물이었다.

취미로 바둑30년 두어왔지만 다른 것은 그렇다치고 승부호흡, 감으로 대변되는 인간만이 할 수 있는 인간만의 특권, 무기는 결코 기계가 따라잡을 수 없는 영역이라는 생각이 들었는데 이것이 눈 앞에서 무너지는 것을 보며 사람이 얼마나 하찮은 존재인지 또 나름 쌓아올린 편견과 개념이라는 것들이 바라보는 프레임에 따라 얼마나 보잘 것 없는 것인지를 여실히 느낄 수 있었던 신선한 추억이었다.

이 책 3장에서 다루는 최적화는 알파고와 같은 AI에 없어서는 안 될 핵심 개념이다.

똑같은 길이의 실로 최대한 넓은 사각형을 만들려면 가로, 세로의 길이가 어느 정도가 적정할까?

실의 길이를 L이라 가정하면 가로 길이와 세로 길이의 합은 L/2가 될 것이고 이를 도식화하면 아래와 같은 책의 설명으로 쉽게 답을 낼 수 있다.

가로를 늘려야 사각형 면적이 커질텐데 이를 늘리면 세로가 줄어들고, 마찬가지로 세로를 늘리자니 가로가 줄어든다. 이 애매한 트레이드 오프 관계에서 최상의 답을 찾아내는 것 그것이 바로 최적화다.

그런데 약간의 흥미를 자극하는 이 퀴즈가 AI랑 도대체 무슨 상관이란 말인가? 그 상관이 무엇인지 설명하는 과정이 이 책의 3장에 잘 정리되어 있고 이런 부분이 이 책의 장점이라 가치라 할 수 있다.

AI는 주로 미래를 예측하는데 쓰인다. 알파고에 쓰인 핵심 기술 중 하나가 딥러닝이라는 것인데 딥러닝은 머신러닝의 일부이고 머신러닝 중 자주 활용되는 선형회귀는 통계학 뿐만 아니라 머신러닝에서도 자주 활용되는 개념이다.

예를 들면 책에 등장한 그림과 같이 아파트 가격을 예측하는 모델을 들 수 있겠다. 아파트 면적이 넓을수록 일반적으로 가격이 높아진다는 사실을 우리는 이미 알고 있지만 과거 데이터를 가지고 있다면 데이터의 추세를 파악하여 어느정도 신뢰할만한 가격 예측 공식을 추출할 수 있다.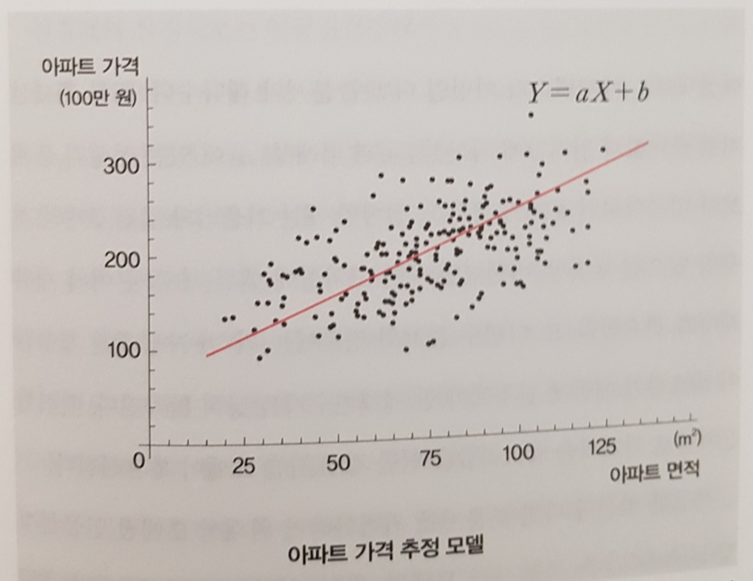

주어진 데이터로부터 면적, 가격의 좌표를 산점도로 나타내면 위 그림의 점의 분포를 나타내게 되고 일반적으로 이는 빨간색의 직선과 같은 추세를 가진다는 사실을 알 수 있는데 구체적으로 이 빨간선을 어떻게 찾아낼 수 있을까?

이 빨간선을 임의로 그려보고 이 선과 각 좌표간의 차이 즉, 오차를 찾아내 그 거리를 모두 합하면 오차의 총합이 된다. 빨간선이 변화하면 오차 합 역시 달라지게 되는데 빨간선의 변화에 따른 오차합의 변화는 함수로 나타낼 수 있다.

이를 목적함수 혹은 손실함수라 표현하며 이 함수의 결과값을 최소화하는 과정에 최적화가 활용된다. 구체적으로는 아래 그림과 같이 경사하강법이라는 기술을 활용하여 보다 빠르게 최적값을 찾아낼 수 있다.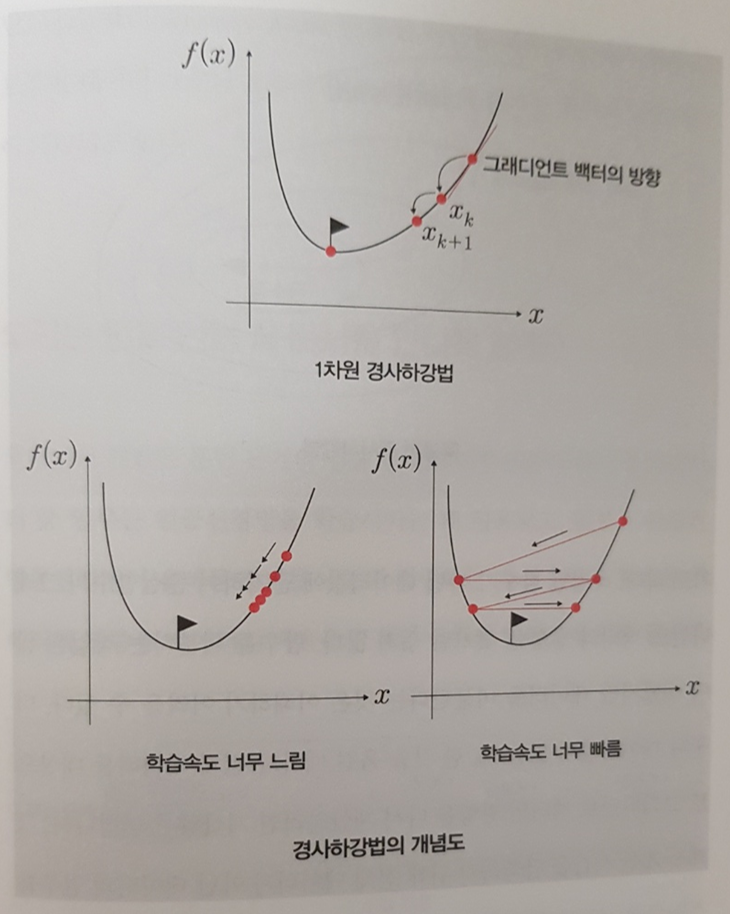

이렇게 최적값을 찾아내면 빨간선이 정해지는 셈이다. 그 빨간선으로 이젠 아파트 평수에 따른 가격을 예측할 수 있게 된다. 이 선형회귀의 예제는 가장 간단한 AI 모델을 설명한 것이지만 아파트 가격을 결정하는 변수는 평수만은 아닐 것이다.

브랜드, 학군, 교통 등 수 많은 변수가 존재할 텐데 이 변수들 간 가격을 결정짓는 최적의 빨간선들이 존재할 것이고 이들이 통합되었을때 최선의 빨간선을 찾는 과정이 AI가 학습을 통해 모델을 찾아내는 과정이다.

이 때 손실함수에서 손실값을 0으로 만드는 지점 즉, 최적값을 찾아내는 과정에 미적분이 활용된다. 이 일련의 과정에서 학교에서 미적분이 무엇인지 계산을 어떻게 하는지에 중점을 두고 학습했던 과거가 야속하다.

목적지가 어딘지도 모르고 왜 이것을 배워야 하는지 알지도 못한채 무작정 좋은 대학, 직장가자고 이유도 없이 노력했던 과정보다는 일상에 어떤 것을 해결하기 위해 또 나의 어떤 목표를 달성하고자 미적분을 그 해결을 위한 도구로 여겼다면 미적분을 익히는 과정이 이를 다루는 과정이 그리 의미없지는 않았을 것이다.

이 책은 바로 미적분을 배우는 의미를 충만하게 해주는 책이다. 나아가 구체적으로 우리 삶에 무언가를 나아지게 하기 위해 수학의 쓸모를 궁리하고 적용할 수 있는 실마리를 안겨주는 책이다.

책의 수준은 수학 교양서와 전공서의 중간 즈음이다. 아주 쉽게 읽한다 할 수는 없겠으나 책의 끝까지 읽어가며 일련의 미적분의 쓸모를 탐험하는데 큰 무리가 드는 책은 아니다.

하지만 수학에 전혀 관심이 없는 독자 혹은 수학에 자신이 없는 독자가 읽기에 쉬운 수준은 아니다. 다만 쓸모라는 키워드를 중심으로 전반적으로 수학이 이런 방식으로 공학이나 일상에 활용된다는 사실이나 감을 잡는데 무리는 없을 것이니 이 책으로 큰 쓸모의 흐름을 익히고 보다 쉬운 수학 교양서로 부족한 부분을 채우는 것도 나름의 독서법으로 쓸 수 있을 것이다.

반면 수학에 나름 자신이 있고 상당한 수준의 기본기를 익힌 독자라면 수학을 제대로 다룰 수 있는 새로운 지평을 얻게 될 것이다.

독자의 수준을 뛰어넘어 이 책은 수학에 대한 새로운 안목이나 프레임을 갖게 해주는 멋진 양서이다.

수학을 수학 그 자체로 보던 과거의 관점을 잠시 접어두고 내 필요에 의한 도구이자 다른 목적을 달성하는데 큰 도움을 주는 동반자로 인식할 수 있는 계기를 만들어준 멋진 책을 가급적 많은 독자들이 읽기 바라는 마음으로 리뷰를 마친다.

---

• 책소개 - 미적분의 쓸모

YES24 리뷰어클럽 서평단 자격으로 작성한 리뷰입니다.