[리뷰] 딥러닝을 위한 수학
in Review on Review, Book, 딥러닝, 수학, 확률, 통계, 선형대수, 미분, 행렬미분, 데이터흐름, 역전파, 경사하강법

제이펍출판사의"딥러닝을 위한 수학(로널드 크노이젤 저/류광 역)"를 읽고 작성한 리뷰입니다.

역전파와 경사하강법 도출을 위해 필요한 최소한의 수학을 유기적으로 잘 엮어나간 딥러닝 도서
본 번역서와 원서 모두 제목만 놓고 봤을때는 딥러닝에 쓰이는 수학을 근원적으로 파헤치는 인상을 받게되지만 모두 읽고 난 후 드는 개인적인 생각으로는 “역전파와 경사하강법을 위한 최소한의 수학“이라고 표현하는 것이 정확할 것 같다.
최소한의 수학이라고 표현한데는 엄밀한 증명의 과정이 빠져있고 심지어는 논문에 자주 인용되는 알고리즘이나 경사하강법의 개선 방법에 쓰이는 도출 과정 등도 생략이 되어있기 때문이다. 
대신 도출 과정이 생략된 최종 공식이 무엇을 의미하는지 그리고 그 공식이 경사하강법이나 역전파에 어떻게 활용되는지 그 흐름을 끊지 않으려는 노력이 돋보이는 책이다.
책의 내용을 설명하기에 앞서 책이 다루는 범위를 명확히 한정짓고 난이도를 민감하게 언급하는 것은 대상 독자의 수준에 따라 호불호가 크게 갈릴 수 있다는 생각이 들었기 때문이다.
오차 역전파법이나 경사하강법은 딥러닝의 입문자에게는 쉽지 않은 주제이지만 딥러닝 분야의 논문을 출판하는 연구자에게는 사칙연산에 가까운 기본 개념이다.
이 책은 전자 수준의 독자에게는 큰 흐름을 유기적으로 이해하는데 도움이 되는 책이고 스스로의 연구를 확장하는데 기초를 잡기에 매우 좋은 책이지만 후자 수준의 독자에게는 큰 도움이 되지 않을 것이다.
딥러닝 입문자 혹은 중고교 수학을 뗀 후 AI에 관심을 가지는 학생 혹은 AI분야의 진로를 정한 학부생에게는 큰 도움이 될 것 같다.
이 책의 가장 큰 장점으로는 앞서 언급한 바와 같이 역전파와 경사하강법을 향한 유기적인 구성이라는 생각이 든다. 보통 다른 책에서는 역전파와 경사하강법의 수학적 공식과 기본적인 개념 및 소스코드 구현 정도로 설명을 끝내는 경우가 많은데 이 책은 보다 이해의 흐름을 중요시 하는 느낌을 받았다.
대표적으로 9장 “합성공 신경망의 데이터 흐름”이 그런 역할을 하는 장이다. 역전파와 경사하강법의 정의도 중요하지만 이 기능이 어디에 어떻게 쓰이는지 정의에 앞서 용도를 파악한 후 정의를 이해해나간다면 보다 이해가 수월할 것이다. 즉, 지도를 갖고 탐험하는 셈이다.
예를 들면 CNN에 쓰이는 합성곱 층이나 풀링 층의 개념이 소개되며 자연스럽게 딥러닝 데이터의 전반적인 흐름을 파악할 수 있으며 그 과정에서 경사하강법이 왜 쓰이는지 어느 부분에서 쓰이는지 감을 잡을 수 있다. 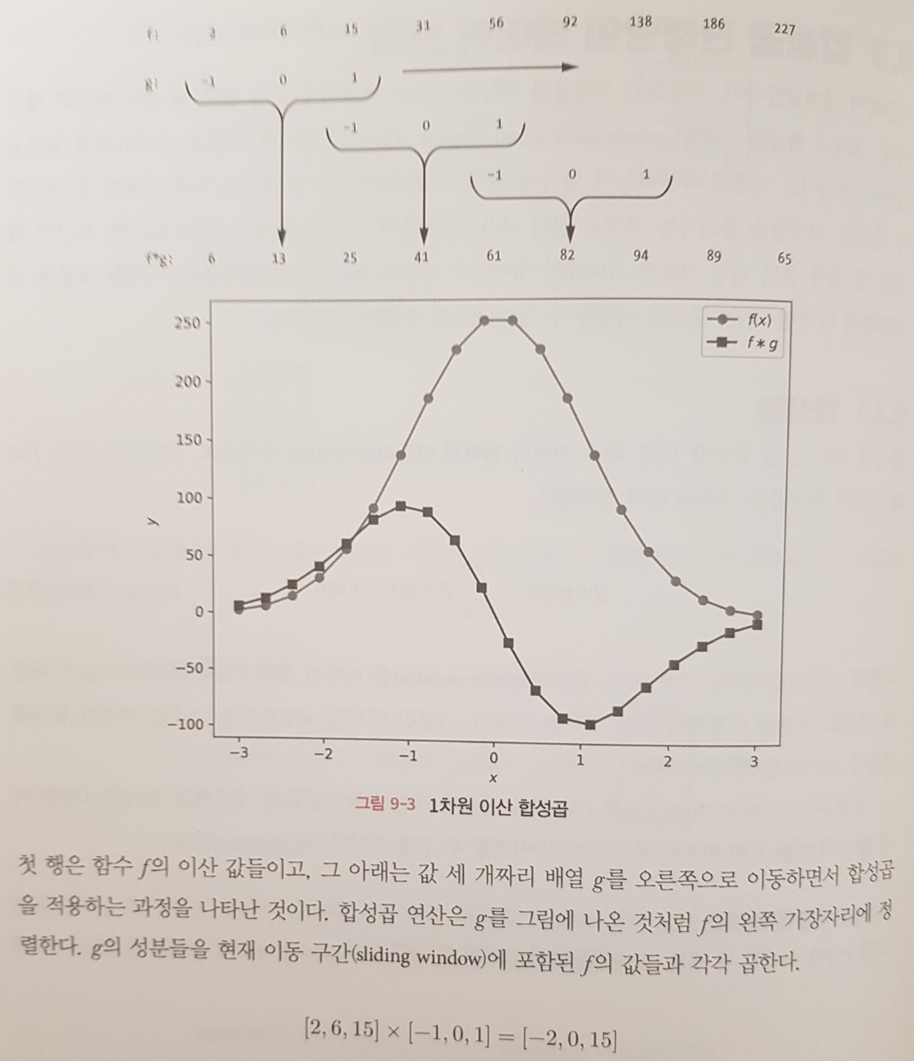
또, 8장의 행렬 미분 파트의 경우에서도 활성화함수의 도함수를 구하는 과정에 필요한 수학을 자연스럽게 유도해 나가고 있으며 6장 행렬 2부 파트에서도 유사 역행렬을 유도해보며 역전파에 쓰이는 도구들에 대한 감을 잡기 쉽게 구성되어있다.
즉, 책의 순서에따라 하나하나의 파트에 집중해서 충실하다보면 자연스럽게 역전파나 경사하강법을 이해하가에 필요한 내공과 감이 축적되어 나가는 셈이고 끝에 다다른 어느 순간 나도 모르는 사이에 “아, 수학이 이렇게 AI와 연결되는 구나!“라는 깨달음을 느낄 수 있도록 구성된 점이 장점이라 할 수 있다.
지식 그 자체를 전달하는 것보다 논리적으로 창의적인 무언가를 도출해내는 데 흐름이나 감을 잡을 수 있다는 것이 장점이다. 물론 그 과정에서 지식 전달 차원에서도 야코비 행렬이나 AdaGrad와 같은 논문에서 흔히 등장하는 기본 개념들을 잡을 수 있어 연구에 관심이 있는 초보자들에게도 적합한 책이 될 것 같다는 생각이 든다.
실습환경을 설정하는 1장이나 확률과 통계를 다루는 2 ~ 4장의 경우 직접적으로 딥러닝과 연관되는 것은 아니므로 이 책은 크게 4장 이전의 전반부와 그 뒤의 후반부로 나눌 수 있다.
전반부의 경우도 딥러닝과 관련은 없지만 어느 정도 개념을 알아야 데이터 과학 전반에 대한 매끄러운 이해가 가능한 부분이고 특히 통계와 접목된 논문을 이해하는데 도움이 되기 때문에 꼭 익혀둘 필요가 있다. 다행히 매우 기초적인 부분만 다루고 있어 이해하는데 큰 어려움이 없다.
초보 연구자에게는 수학이라는 도구를 통해 역전파와 같은 유용한 AI 도구의 아이디어를 착상하는 일련의 감각과 흐름을 형성하는데 도움이 될 것이며, 딥러닝 입문자에게는 수학으로 인한 큰 스트레스 없이 딥러닝의 핵심이라 할 수 있는 역전파와 경사하강법을 이해하는데 큰 도움이 될 것이다.
