이지북 출판사의 "미르카, 수학에 빠지다 5(유키 히로시 저/김소영 역/남호영 감수)"를 읽고 작성한 리뷰입니다.

---

거인이 쌓아온 위대한 수학에 활용된 아이디어, 추론 방식, 통찰 과정을 쉽게 소설로 이해할 수 있는 명작. 사다리타기라는 간단한 문제를 시작으로 군, 체, 공리, 갈루아 논문에 이르는 진리탐구로 향하는 문을 열 수 있는 기회를 얻을 수 있었다.

보석같은 책이다. 수학을 좋아하는 나는 집에 100권이 넘는 수학책을 갖고 있다. 그마저도 보석같은 책만을 남겨두고 정리한 것만 100권이 넘는데도 그 중에서도 하나를 고르라면 적어도 현재 내 수준이라는 조건에서는 이 미르카 시리즈를 고를 것이다.

그간 수백권이 넘는 책의 리뷰를 남겼지만 책 소개에 앞서 극찬을 남기는 경우는 매우 드물었다. 간만에 그런 명작을 만나게 되었고 예상과는 달리 3개월의 정독을 더 한 후에야 리뷰를 작성하게 되었다.

그만큼 이런 명작의 리뷰를 남기는 것은 늘 부담이다. 깊이 있는 지혜를 온전히 이해하지 못했기 때문이고 그만큼 책을 비평하거나 칭찬할만한 실력이 받쳐주질 못하기 때문이다.

그렇지만 적어도 이 책이 고수들이 머무는 진리의 세계를 여는 문은 된다고 확신한다. 이미 갈루아와 관련된 잉여군, 확대체, 군지수, 확대차수, 정규부분군, 가해군, 갈루아 대응 등 하나하나 수준 높은 지식을 책에서 다루고 있음에도 무한한 진리의 세계와 비교한다면 사칙 연산의 수준에 지나지 않을 것이기 때문이다.

이 책에 등장하는 지식의 양은 너무도 거대해서 오히려 이 내용들을 한 권의 책으로 축약한 저자의 능력에 감탄할 뿐이다. 그렇기에 이 위대한 압축본을 리뷰로 또 압축하는 것은 불가능이다.

갈루아와 군론에 대한 내용도 소개하기 어려우니 책에 등장한 간단한 문제 하나로 감을 잡게 하는 정도가 내가 표현할 수 있는 수준의 한계다.

x^2 - 1

위 식은 인수분해 할 수 있을까? 고등학교까지의 정규과정을 마친 사람이라면 쉽게 답을 낸다. 답은 (X+1)(x-1). 인수분해 중에서도 가장 쉬운 처음으로 등장하는 문제이기 때문이다. 덕분에 방정식의 해도 구할 수 있다.

그렇다면 아래의 식은 인수분해가 가능할까?

x^2 + 1

보자마자 불가능하다고 답할 독자가 99%이다. 선생님이 불가능하다고 하셨고 시험 문제로도 나오지 않기 떄문에 나도 고정관념처럼 이 문제는 인수분해가 불가능하다고 확신했다.

하지만 답에 허수를 표기할 수 있다면 얘기는 달라진다. (X+i)(X-i)로 풀 수 있기 때문이다. 기억이 가물거리는 분들을 위해 허수 i를 소개하자면 제곱해서 -1이 되는 수이다.

즉, 이 문제는 다음과 같이 정리할 수 있다.

• 유리수체 Q 위에서 기약이다.
• 복소수체 C 위에서 가약이다.

눈치빠른 사람은 감이 올 것이다. 갈루아, 군론 이 개념들은 활용할 수 있는 수의 범위가 있다는 것을. 위에서 정리한 “체“라는 것은 연산이 가능한 수의 집합체를 의미한다.

수학의 세계에 어느정도의 공리와 체, 군을 활용하느냐에 따라 해의 존재여부는 극명하게 달라진다. -1에 제곱근을 취해 실수로 표현불가능한 i 허수가 생겼듯, 새로운 연산을 기존의 수에 적용하면서 수의 세계는 점점 넓어진다.

갈루아를 주제로 다룬 책이기때문에 독자들을 위해 결론을 그것도 가장 쉽게 설명하는게 리뷰의 의무일 것 같아 이 간단한 질문을 먼저 소개하였지만 사실 이 문제는 책의 후반부에 등장한다.

그 10장에 이르기까지 사전에 흥미를 잃지 않고 자신감을 잃지 않도록 거인의 어깨까지 지식을 차곡차곡 소설으로 읽으며 쌓아올릴 수 있다는 점은 이 책의 가장 큰 매력이다.

수학의 세계에서 거인들이 진리를 찾아 떠난 모험의 방식을 배울 수 있다는 것이 갈루아나 군론을 이해하는 것 보다 더 큰 수확일지도 모르겠다.

첫장은 단순한 문제로 시작한다. 누구나 쉽게 그리는 사다리 타기. 아래 그림에서 사다리를 총 몇개나 그릴 수 있을까?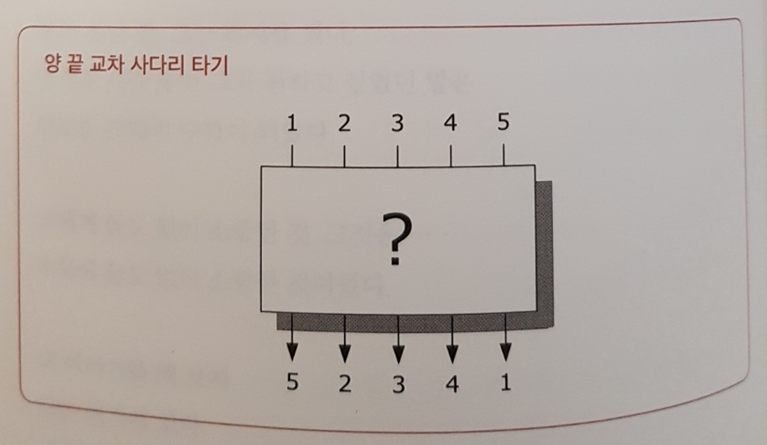

답이 중요한 것이 아니라 그 안의 온전한 연역 규칙과 논리를 세워나가는 것이 중요하다. 그렇게 쌓인 실력은 어떤 분야에서도 세상에 알려지지 않은 지식의 경계선을 넓혀나가는 행위 즉, 진리를 찾는 여정에 든든한 자산이 되기 때문이다.

처음엔 마구잡이로 그리면서 시작하겠지만 종국에는 동일한 패턴을 발견하면서 일종의 연산 규칙이 표준화된다. 우리의 직감이 꽤 도움이 된다. 정리하자면 다음과 같은 연산이 정리된다. 연산이 정리되면 기존의 수학을 이용할 수 있게된다.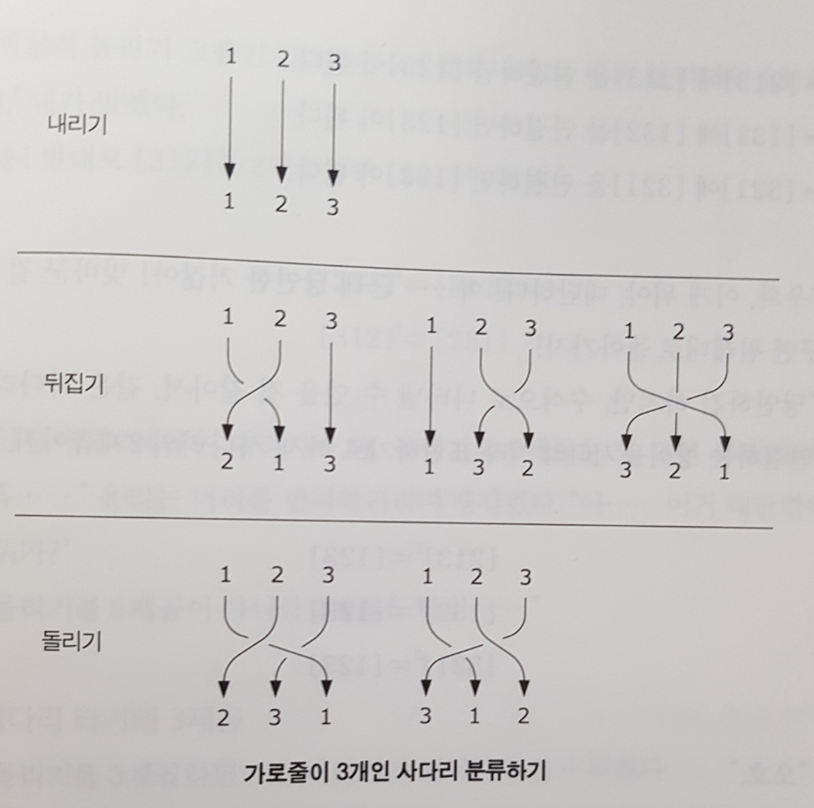

문제를 정의하고, 정의된 문제로 도출하는 과정을 해석가능하게 정리하는 능력은 논문을 쓰는데 있어, 나아가 진리탐구에 있어 큰 초석을 다지는 행위이다.

또, 이 책에서는 갈루아의 첫번째 논문과 군, 체 등을 이해하는데 큰 도움이 되는 과정이다. 이렇게 쉬운 문제로 독자로 하여금 갈루아가 깨달았던 감각까지 이끌어준다는 구성에 감탄을 금치 못했다.

또 하나의 재미있는 예시를 들겠다. Root a는 그림으로 그릴 수 있을까? 보통 끝없는 소수점으로 이어지는 무리수를 과연 그림으로 표현할 수 있냐는 말이다. 보통 직관적으로는 불가능한 답이라고 생각할 수 있겠으나 다음 그림을 참고하면 경이롭다.

이렇듯 그림으로 그릴 수 있느냐의 여부는 또 다른 중요한 문제가 된다. 또한 꼭 이 책의 이해를 위한 목적을 넘어서서 기하학이라는 또 다른 수학의 커다란 세계의 호기심을 여는 장이 되기도 한다는 것이 중요한 부분이다.

위에서 언급한 군, 체의 감각은 공리를 통해 정리될 수 있으니 호기심 자극 차원에서 책의 군의 공리 내용을 소개해본다.

책의 후반부에 소개되는 천재 갈루아의 생애가 안타깝다.

거듭제곱근으로 방정식을 풀 수 있는 조건에 대한 논문 (방정식을 대수적으로 풀기 위한 필요충분조건)

갈루아의 첫번째 논문의 제목이다. 그는 만 채 21세가 되기 전에 세상을 떠났기에 그의 논문은 몇 되지 않는다. 그럼에도 수학의 새로운 세계를 연 셈이니 천수가 허락하는 일반인들 정도의 생애를 살았다면 수학사에 어떤 일이 벌어졌을지 상상이 가지 않는다.

참으로 감사하게도 이 책의 저자는 친절히 이 첫 논문을 최대한 쉽게 풀어서 설명하고 있다. AI와 선형대수를 공부하며 교과서로 군론을 접했을 때 머리가 많이도 빠졌던 것 같은데 이 책은 신기하게도 그런일이 없었다.

물론 이해하는데 시간도 오래걸리고 쉽진 않았지만 탐험 내내 늘 즐거웠고, 생각의 발전을 위해 시간을 낭비했을지언정 기존처럼 이해 자체가 되지 않아 헛된 시간을 보낸 일은 없다.

수학사 혹은 수학의 빛을 받는 어떤 분야 혹은 진리 탐구 그 자체를 위해서라도 누구에게나 큰 힘이 되어줄 수 있는 명작이다. 신이, 자연이 만든 세상의 진리를 진정성있게 들여다 볼 수 있게 해주는 위대한 책이다.

일본식 특유의 미소녀가 소설에 등장하며 언뜻보기에 책의 수준이 우스워보일지도 모르겠으나 적어도 내게는 위대한 저자가 자신의 명작을 겸손하게 표현한 흔적으로 보일 뿐이다.

특히 자라나는 청소년들이 이 책을 읽게된다면 그 꼬리에 꼬리를 무는 잠재력이 어디까지 뻗칠 수 있을지 가히 상상이 가질 않는다. 적어도 나는 반드시 이 책을 아들에게 읽힐 생각이다.

본 시리즈가 아직도 5권이나 남아있다는 것이 행복하다. 시간이 허락하는대로 한 권씩 모두 독파하고 리뷰를 남겨보겠다.

---

• 책소개 - 미르카, 수학에 빠지다 5

YES24 리뷰어클럽 서평단 자격으로 작성한 리뷰입니다.